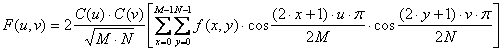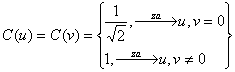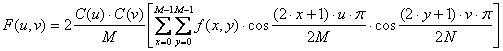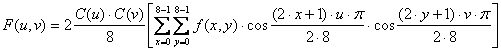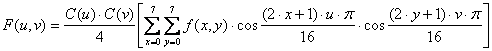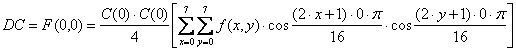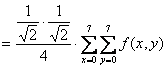5. JPEG NORMA

TEMELJNI KODER

PODIJELA SLIKE NA BLOKOVE

DISKRETNA KOSINUSNA TRANSFORMACIJA

KVANTIZACIJA

CIK-CAK ANALIZIRANJE

DPCM

KODIRANJE DULJINE NIZA

ENTROPIJSKO KODIRANJE

Diskretna kosinusna transformacija

Nakon podijele slike u blokove slijedi postupak transformacijskog kodiranja. Prvi korak transformacijskog kodiranja je transformacija. JPEG norma rabi dvodimenzijsku diskretnu kosinusnu transformaciju (DCT - Discrete Cosine Transform). 1974. godine Ahmed, Natarajan i Rao dokazali su da DCT daje optimalne rezultate u pogledu zadovoljenja osnovnih uvjeta koje transformacija treba zadovoljiti. DCT je slična diskretnoj Fourierovoj transformaciji (DFT-Discrete Fourier Transform), ali za razliku od nje ima realnu jezgru i nema redudantnih kompleksno-konjugiranih parova. Jezgra transformacije je jednaka za sve blokove što omogučuje veću brzinu proračunavanja DCT-a. DCT je odvojiva transformacija što znači da se može provoditi zasebno za horizontalni i vertikalni smjer. DCT transformacija koristi kosinusne funkcije čiji su argumenti diskretni valni oblici .

Definicija DCT transformacije opisana je izrazom (5.8), a njoj inverzna transformacija (IDCT) izrazom (5.9) [6].

,

(5.8)

,

(5.9)

pri čemu su M i N broj redaka i stupaca matrice nad kojom se vrši DCT. je diskretna vrijednost elemenata slike u bloku s koordinatama xy, prema slici 5.4. Kao rezultat DCT-a nastaje matrica s vrijednostima transformacijskih koeficijenata s koordinatama uv. C(u) iC(v) su konstantni članovi i iznose:

,

(5.10)

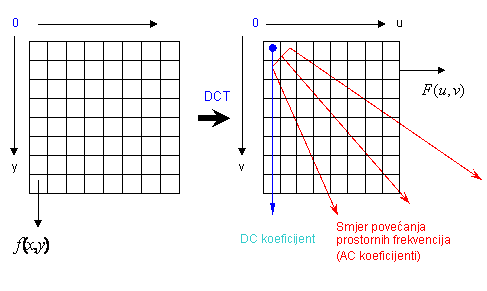
Slika 5.4. Ulazni i izlazni parametri DCT transformacije

Kod JPEG-a se rabi kvadratna matrica veličine 8x8 elemenata slike. Ako u izraz (5.8) uvrstimo, slijedi:

,

(5.11)

,

(5.12)

što daje konačan izraz za DCT transformaciju:

,

(5.13)

Sličnim razmatranjem dobije se konačan izraz za inverznu DCT transformaciju:

,

(5.14)

Slika 5.5. [6] pokazuje osnovne valne oblike 8x8 DCT transformacije pri čemu mjesto valnog oblika u slici odgovara mjestu koeficijenta u DCT bloku.

Slika 5.5 Osnovni valni oblici DCT transformacije

Iz izraza (5.13) uočljivo je da DCT za određivanje svakog DCT koeficijenta, prolazi kroz sve elemente bloka. Da bi se dobio jedan DCT koeficijent, potrebno je 8x8=64 operacija što za sva 64 DCT koeficijenta odnosno jedan cijeli blok daje ukupno 4096 operacija. Za cijelu sliku veličine 256x256 elemenata slike potrebno je: 1024 (blokova) * 4096 (operacija po jednom bloku) što daje 4 194304 operacija. To je prihvatljiv hardverski zahtjev. Ako bi blok bi jedak dimenziji slike od 256x256 elemenata slike tada bi broj operacija bio oko 1025 puta veći. Kako je brzina transformacije jedan od bitnih svojstava, blok 8x8 smatra se idealnim za diskretnu kosinusnu transformaciju. DCT koeficijenti, , sadržavaju informaciju o frekvencijskom sastavu slike. Koeficijent zove se istosmjerni ili DC koeficijent i nalazi se u lijevom gornjem uglu transformacijske matrice. DC koeficijent jednak je osmerostrukoj srednjoj vrijednosti svih DCT koeficijenata. To se može dokazati uvrštavanjem u izraz (5.13) , čime se dobije:

,

(5.15)

,

(5.16)

,

(5.17)

Srednja vrijednost elemenata slike iznosi:

,

(5.18)

Usporedbom izraza (5.17) i (5.18) slijedi da je , čime je dokaz završen.

DC koeficijent sadrži najveći dio informacije o slici i najbitniji je za rekonstrukciju slike. Ako bi blok sadržavao jednake vrijednosti, tada bi od svih DCT koeficijenata DC koeficijent bio jedini različit od nule. On bi nosio cijelu informaciju o slici. Preostala 63 koeficijenta nazivaju se izmjeničnim ili AC koeficijentima. AC koeficijenti sadržavaju informaciju o prostornim frekvencijama u bloku odnosno u slici. Prema slici 5.4. u smjeru povećanja koordinata u,v, smanjuje se vrijednost AC koeficijenata. Pri tome AC koeficijenti koji se nalaze u okolini DC koeficijenta odgovaraju nižim prostornim frekvencijama, a AC koeficijenti koji se smješteni prema donjem desnom uglu opisuju više prostorne frekvencije. DCT transformacija na temelju frekvencijske analize nad elementima bloka, provodi preraspodjelu energije koju nosi pojedini element u bloku. Najveći dio energije koncetriran je u DC koeficijentu te niskofrekvencijskim AC koeficijentima koji ga okružuju. AC koeficijenti nižih prostornih frekvencija nose više korisne informacije nego oni viših frekvenija. Ovakav način koncetracije energije u skladu je sa svojstvom ljudskog vizualnog sustava. DCT visoke frekvencije prikazuje, po apsolutnoj vrijednosti, malim brojevima koje se onda kodiraju s manjom preciznošću.

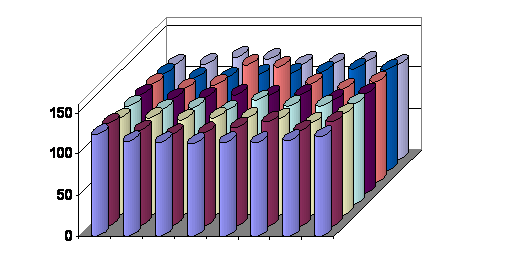
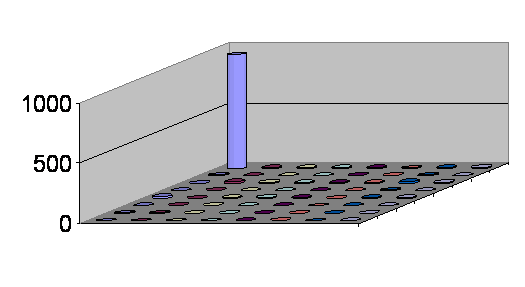
Iz ispitne slike «Baboon» odabrana su dva bloka označeni na slici 5.3. U tablici 5.1 i na slici 5.6 prikazane su amplitude elemenata slike u bloku «A». Uočljivo je da su sve amplitude u rasponu 110 do 141, te da su susjedne vrijednosti slične. U bloku nema naglih prijelaza što znači da visokofrekvencijski koeficijenti poprimaju male vrijednosti što je vidljivo u tablici 5.2. Na slici 5.7 se vidi da je većina energije bloka sadržana u DC koeficijentu. Amplitude bloka «B» prikazane su tablicom 5.3. i na slici 5.8. Amplitude elemenata slike u bloku «B» se nalaze u rasponu od 43 do 200, a razlika između susjednih elemenata slike je vrlo velika. 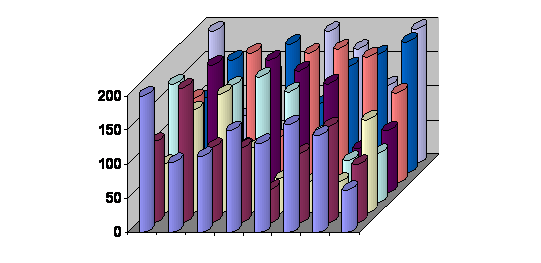Blok «B» sadrži nagle prijelaze što generira visoke prostorne frekvencije, pa su vrijednosti visokofrekvencijskih DCT koeficijenta relativno velike (tablica 5.4). Na slici 5.9. se vidi da većinu informacije i u ovom bloku nosi DC koeficijent. Međutim svi preostali DCT koeficijenti imaju, po apsolutnoj vrijednosti, znatno veće vrijednosti nego oni u bloku «A», posebice visokofrekvencijski DCT koeficijenti.

Tablica 5.1. Amplitude elemenata slike bloka «A»

123	115	114	112	114	114	116	121
123	115	110	112	118	125	115	125
116	117	115	117	117	116	111	122
118	114	116	112	125	118	118	121
119	114	115	119	117	118	112	120
118	112	117	141	139	119	113	121
117	112	113	116	117	120	123	122
115	116	125	122	115	116	118	115

Slika 5.6. Amplitude elemenata slike bloka «A»

Tablica 5.2 Prikaz DCT koeficijenata bloka «A»

942.6	-7.2	-1.5	2.5	14.6	-2.2	5.1	-0.7
-6.3	0.4	14.6	5.8	0.0	-7.1	3.5	-0.6
-2.7	1.4	7.5	-1.3	-7.4	5.2	0.7	-0.3
5.7	-0.6	-5.9	2.6	10.9	2.3	-2.2	-1.6
-5.9	5.4	5.0	-2.9	-7.4	2.1	1.3	4.8
-2.3	-4.0	4.1	0.7	-2.1	0.3	-3.2	5.7
4.2	7.0	-13.3	-8.2	7.3	0.7	-3.3	-0.8
-9.3	1.8	9.2	-3.2	-5.8	1.4	1.7	-3.8

Slika 5.7. Prikaz DCT koeficijenata bloka «A»

Tablica 5.3. Amplitude elemenata slike bloka «B»

200	102	111	149	131	158	142	62
118	197	110	108	49	101	140	85
71	150	174	94	50	46	44	136
174	66	172	185	163	101	62	72
43	187	66	195	178	160	65	91
124	67	191	68	190	196	185	132
109	166	101	189	102	155	173	192
194	68	129	127	193	167	114	197

Slika 5.8. Amplitude elemenata slike bloka «B»

Tablica 5.4. Prikaz DCT koeficijenata bloka «B»

1029.6	22.0	-42.1	6.4	13.1	0.6	22.7	-20.0
-102.0	118.5	15.6	-17.4	-50.8	31.9	-34.2	-17.2
55.1	-31.9	95.4	54.8	6.3	49.0	6.2	1.4
56.2	-55.1	-45.9	93.7	-50.5	18.4	-33.5	-2.4
26.4	33.5	-86.8	85.6	107.9	12.6	22.6	-3.4
23.3	14.3	-1.2	-17.2	38.3	66.5	30.3	12.5
-11.0	-19.8	2.5	9.9	3.2	-8.2	95.6	105.9
-36.0	-5.3	-3.1	-62.5	-8.2	-67.7	-69.4	-107.2

Slika 5.9. Prikaz DCT koeficijenata bloka «B»

Ako bi amplitude svih elemenata slike u bloku bile jednake, tada bi svi AC koeficijenti bili jednaki nuli i informacija koju nosi blok bila bi sadržana u DC koeficijentu. DCT transformacija nad ispitnim blokovima «A» i «B» provedena je pomoću programa DCTlab razvijenog na Zavodu za radiokomunikacije i visokofrekvencijsku elektroniku Fakulteta elektrotehnike i računarstva u Zagrebu. Važno je istaknuti da DCT transformacija ne unosi gubitke, dapače čak i povećava količinu bitova potrebnih za prikaz DCT koeficijenata. Amplitude elemenata slike u bloku prikazane su s 8 bitova, tj. najveća amplituda je 255 (maksimalno bijelo). Najniža amplituda je 0 i označava crno. Amplitude od 1 do 254 su tonovi sivog. Vrijednosti DC i AC koeficijenata mogu biti puno veće što se vidi iz tablice 5.2, pa je potrebno više od 8 bita za njihovo prikazivanje. Općenito gledajući, DCT koeficijenti su realni brojevi koji mogu biti i s negativnim predznakom. Negativne vrijednosti posljedica su djelovanja kosinus funkcije. Kako bi se u dekoderu mogla provesti dekompresija slike, nužno je postojanje inverzne diskretne kosinusne transformacije (IDCT). IDCT omogućuje vraćanje u prostornu domenu.

Kod DCT-a i IDCT-a, jedini gubici koji se javljaju su posljedica proračunavanja kosinus funkcije. Iz izraza (5.13) se vidi da DCT radi s kosinus funkcijama. Kosinus je trascendentna funkcija i prikazuje se pomoću Taylorovog reda:

,

(5.19)

,

(5.20)

Dakle nemoguće je apsolutno točno izračunati vrijednost funkcije kosinus za bilo koji realan broj. No smatra se da je aproksimacija s već nekoliko članova reda zadovoljavajuća, te da ljudsko oko radi toga neće vidjeti pogrešku na rekonstruiranoj slici.

Mana sustava kompresije temeljenih na DCT-u je pojava vidljivih rubova blokova u rekonstruiranim slikama, a koja nastaje zbog podijele slike u blokove. Prirodne slike nisu sastavljene od objekata pravilnih kontura, pa ljudsko oko zamjećuje konture blokova u rekonstruiranoj slici pri većim stupnjevima kompresije.

ÛPodijela slike na blokove

KvantizacijaÜ

MENTOR:

Prof.dr.sc.Sonja Grgić

Û prethodno poglavlje Û

Ü slijedeće poglavlje Ü

Autor:

Mihael Jančić